Usaha Dan energi
Bentuk Energi dan Perubahannya
Energi (disebut juga tenaga) adalah kemampuan untuk melakukan usaha.
Energi (disebut juga tenaga) adalah kemampuan untuk melakukan usaha.
Bentuk-Bentuk Energi
a) Energi Mekanik
Benda yang bergerak atau memiliki kemampuan untuk bergerak, memiliki energi mekanik. Air terjun yang berada di puncak tebing memiliki energi mekanik yang cukup besar, demikian juga dengan angin.
a) Energi Mekanik
Benda yang bergerak atau memiliki kemampuan untuk bergerak, memiliki energi mekanik. Air terjun yang berada di puncak tebing memiliki energi mekanik yang cukup besar, demikian juga dengan angin.
b) Energi Bunyi
Energi bunyi adalaj energi yang dihasilkan oleh getaran partikel-partikel udara disekitar sebuah sumber bunyi. Contoh : Ketika radio atau televisi beroperasi, pengeras suara secara nyata menggerakkan udara didepannya. Caranya dengan menyebabkan partikel-partikel udara itu bergetar. Energi dari getaran partikel-partikel udara ini sampai ditelinga, sehingga kamu dapat mendengar.
c) Energi kalor
Energi kalor adalah energi yang dihasilkan oleh gerak internal partikel-partikel dalam suatu zat. Contoh : apabila kedua tanganmu digosok-gosokkan selam beberapa detik maka tanganmu akan terasa panas. Umumnya energi kalor dihasilkan dari gesekan. Energi kalor menyebabkan perubahan suhu dan perubahan wujud.
d) Energi Cahaya
Energi Cahaya adalah energi yang dihasilkan oleh radiasi gelombang elektromagnetik
e) Energi Listrik
Energi Listrik adalah energi yang dihasilkan oleh muatan listrik yang bergerak melalui kabel.
f) Energi Nuklir
Energi nuklir adalah energi yang dihasilkan oleh reaksi inti dari bahan radioaktif. Ada dua jenis energi nuklir yaitu energi nuklir fisi dan fusi. Energi nuklir fisi terjadi pada reaktor atom PLTN. Ketika suatu inti berat (misal uranium) membelah (fisi), energi nuklir cukup besar dibebaskan dalam bentuk energi kalor dan energi cahaya. Energi nuklir juga dibebaskan ketika inti-inti ringan (misalnya hidrogen) bertumbukan pada kelajuan tinggi dan bergabung (fusi). Energi matahari dihasilkan dari suatu reaksi niklir fusi dimana inti-inti hidrogen bergabung membentuk inti helium.
Energi Mekanik
Energi mekanik adalah energi yang berkaitan dengan gerak atau kemampuan untuk bergerak. Ada dua macam energi mekanik yaitu ; energi kinetik dan energi potensial.
a. Energi kinetik
Energi kinetik adalah energi yang dimiliki benda karena geraknya atau kelajuannya. Energi kinetik dirumuskan :
Energi mekanik adalah energi yang berkaitan dengan gerak atau kemampuan untuk bergerak. Ada dua macam energi mekanik yaitu ; energi kinetik dan energi potensial.
a. Energi kinetik
Energi kinetik adalah energi yang dimiliki benda karena geraknya atau kelajuannya. Energi kinetik dirumuskan :
EK = energi kinetik (joule atau J), m = massa (kg), v = kelajuan
b. Energi Potensial
Energi potensial adalah energi yang dimiliki oleh benda karena posisinya. Energi potensial dapat dirumuskan:
EP
= energi potensial gravitasi (joule atau J), m = massa (kg), g =
percepatan gravitasi (m/s2), h = ketinggian benda dari acuan (m).
Konsep Energi dan Perubahannya dalam keseharian
a. Konversi energi
Konversi energi adalah perubahan bentuk energi dari bentuk satu ke bentuk lainnya. Contoh
a. Konversi energi
Konversi energi adalah perubahan bentuk energi dari bentuk satu ke bentuk lainnya. Contoh
b. Konverter energi
Konverter energi adalah alat atau benda yang melakukan konversi energi. Beberapa konverter energi yaitu:
1. Setrika listrik mengubah energi listrik menjadi kalor
2. Ayunan mengubah energi kinetik menjadi energi potensial energi potensial menjadi energi kinetik
3. Rem mobil mengubah energi kinetik menjadi energi kalor.
Konverter energi adalah alat atau benda yang melakukan konversi energi. Beberapa konverter energi yaitu:
1. Setrika listrik mengubah energi listrik menjadi kalor
2. Ayunan mengubah energi kinetik menjadi energi potensial energi potensial menjadi energi kinetik
3. Rem mobil mengubah energi kinetik menjadi energi kalor.
ENERGI
Jika sebuah benda menempuh jarak sejauh S akibat gaya F yang bekerja pada benda tersebut maka dikatakan gaya itu melakukan usaha, dimana arah gaya F harus sejajar dengan arah jarak tempuh S.
USAHA adalah hasil kali (dot product) antara gaya den jarak yang ditempuh.
USAHA adalah hasil kali (dot product) antara gaya den jarak yang ditempuh.
W = F S = |F| |S| cos q
q = sudut antara F dan arah gerak
Satuan usaha/energi : 1 Nm = 1 Joule = 107 erg
Dimensi usaha energi: 1W] = [El = ML2T-2
Kemampuan untuk melakukan usaha menimbulkan suatu ENERGI (TENAGA).
Energi dan usaha merupakan besaran skalar.
Beberapa jenis energi di antaranya adalah:
- ENERGI KINETIK (Ek)
Ek trans = 1/2 m v2 Ek rot = 1/2 I w2
m = massa
v = kecepatan
I = momen inersia
w = kecepatan sudut
- ENERGI POTENSIAL (Ep)
Ep = m g h
h = tinggi benda terhadap tanah
- ENERGI MEKANIK (EM)EM = Ek + Ep
Nilai EM selalu tetap/sama pada setiap titik di dalam lintasan suatu benda.
Pemecahan soal fisika, khususnya dalam mekanika, pada umumnya didasarkan pada HUKUM KEKEKALAN ENERGI, yaitu energi selalu tetap tetapi bentuknya bisa berubah; artinya
jika ada bentuk energi yang hilang harus ada energi bentuk lain yang
timbul, yang besarnya sama dengan energi yang hilang tersebut.
Ek + Ep = EM = tetap
Ek1 + Ep1 = Ek2 + Ep2
ENERGI POTENSIAL PEGAS (Ep)
Ep = 1/2 k D x2 = 1/2 Fp Dx
Fp = - k Dx
Dx = regangan pegas
k = konstanta pegas
Fp = gaya pegas
k = konstanta pegas
Fp = gaya pegas
Tanda minus (-) menyatakan bahwa arah gaya Fp berlawanan arah dengan arah regangan x.
2 buah pegas dengan konstanta K1 dan K2 disusun secara seri dan paralel:
|
seri
|
paralel
|
|
|
1 = 1 + 1
Ktot K1 K2 |
Ktot = K1 + K2
|
Note:
Energi potensial tergantung tinggi benda dari permukaan bumi. Bila
jarak benda jauh lebih kecil dari jari-jari bumi, maka permukaan bumi
sebagai acuan pengukuran. Bila jarak benda jauh lebih besar atau sama
dengan jari-jari bumi, make pusat bumi sebagai acuan.
Energi Potensial Gravitasi
Energi
potensial ini berpotensi untuk melakukan usaha dengan cara mengubah
ketinggian. Semakin tinggi kedudukan suatu benda dari bidang acuan,
semakinbesar pula energy potensial gravitasinya. Usaha untuk mengangkat
benda setinggi h adalah
W = Fs = mgh
Dengan
demikian, pada ketinggian h benda mamiliki energy potensial gravitasi,
yaitu kemampuan untuk melakukan usaha sebesar W = mgh. Jadi, energy
potensial gravitasi dapat dirumuskan sebagai
EP = mgh
Dengan,
EP = energy potensial gravitasi (Joule)
m = massa benda (kg)
g = percepatan gravitasi (m/s2)
h = ketinggian benda dari bidang acuan (m)
Kekekalan Energi
Bunyi
hukum kekekalan energy, Energi tidak dapat diciptakan dan tidak dapat
dimusnahkan, tetapi dapat diubah dari satu bentuk ke bentuk energy lain.
Ebensin <!–[if gte msEquation 12]>?<![endif]–> Ekimia <!–[if gte msEquation 12]>?<![endif]–> Egerak
Emekanik = EK +EP
Emekanik = konstan (kekal), selama tidak ada gaya dari luar.
USAHA
Dalam
fisika, usaha berkaitan dengan suatu perubahan. Seperti kita ketahui,
gaya dapat menghasilkan perubahan. Apabila gaya bekerja pada benda yang
diam , benda tersebut bisa berubah posisinya. Sedangkan bila gaya
bekerja pada benda yang bergerak, benda tersebut bisa berubah
kecepatannya.
Usaha
yang dilakukan oleh suatu gaya adalah hasil kali antara komponen gaya
yang segaris dengan perpindahan dengan besarnya perpindahan. Usaha juga
bisa didefinisikan sebagai suatu besaran scalar yang di akibatkan oleh
gaya yang bekerja sepanjang lintasan.
Misalkan
suatu gaya konstan F yang bekerja pada suatu benda menyebabkan benda
berpindah sejauh s dan tidak searah dengan arah gaya F, seperti
ditunjukkan pada gambar di bawah ini. Komponen gaya yang segaris dengan
perpindahan adalah Fx = F cos ?.
W = Fx . s = (F cos ?) . s = Fs cos ?
dengan :
W = Usaha (joule = J)
F = gaya (N)
s = perpindahan (m)
? = sudut antara F dan s (derajat atau radian)
HUBUNGAN USAHA DAN ENERGI
Usaha dan Energi Kinetik
Usaha yang dilakukan suatu gaya dapat mengubah energy kinetik benda.
W = ?EK = mvakhir mvawal
Catatan : Benda bergerak pada bidang datar atau ketinggian benda tetap.
Pembuktian rumus di atas:
Jika gaya F selalu tetap, maka percepatan a akan tetap juga, sehingga untuk a yang tetap
W1>2 = ?1 F(s) . ds
= ?1 m dv/dt . ds
= ?1 mdv . ds/dt
= ?1 mv . dv
= ?1 mvdv
= mv2 |12 > menggunakan perhitungan integral
= mv2akhir - mv2awal
GERAK HARMONIK
Gerak
harmonic adalah gerak periodic yang memiliki persamaan gerak sebagi
fungsi waktu berbentuk sinusoidal. Gerak harmonic sederhana
didefinisikan sebagai gerak harmonic yangdipengaruhi oleh gaya yang
arahnya selalu menuju ke titik seimbang dan besarnya sebanding dengan
simpangannya.
Periode dan Frekuensi
Periode
menyatakan waktu yang diperlukan untuk melakukan satu siklus gerak
harmonic, sedangkan frekuensi menyatakan jumlah siklus gerak harmonic
yang terjadi tiap satuan waktu.
?F = ma
ky = mw2y
k = mw2
mengingat bahwa w = 2?/T, maka
k = m (2?/T)2
T = 2? ?m/k
Karena f = 1/T, maka diperoleh :
F = 1/2? ?k/m
Dari
persamaan di atas menyatakan bahwa periode dan frekuensi gerak harmonic
pada pegas hanya bergantung pada massa benda dan konstanta gaya pegas.
Konsep Usaha dan Energi
Dalam fisika usaha yang dilakukan oleh sebuah gaya didefinisikan sebagai hasil kali gaya dengan perpindahan benda yang searah dengan gaya. Dapat dirumuskan :
Satuan usaha dalam SI adalah joule. Satu joule adalah besar usaha yang dilakukan oleh gaya satu newton untuk memindahkan suatu benda searah gaya sejauh satu meter.
Kaitan usaha dan energi yaitu besar usaha yang dilakukan oleh suatu gaya dalam proses apa saja adalah sama dengan besar energi yang dipindahkan.
Usaha oleh Beberapa Gaya
Apabila usaha yang dilakukan oleh orang pertama dan orang kedua untuk memindahkan suatu benda ke kanan sejauh s adalah
W1 = F1 s (*) dan W2 = F2 s (**)
Telah diketahui bahwa resultan dua gaya searah adalah F =F1 + F2,
sehingga usaha total yang dilakukan oleh kedua benda tersebut adalah
W = F s, W = (F1 + F2) s
Dengan memasukkan F1 s = W1 (lihat *) dan F2 s =W2 (lihat **), maka diperoleh
W = W1 + W2
Secara umum dapat disimpulkan sebagai berikut :Usaha ynag dilakukan oleh resultan gaya-gaya searah dan berlawanan arah, yang menyebabkan benda berpindah sejauh s, sama dengan jumlah usaha oleh tiap-tiap gaya
Contoh Soal Usaha & Energi 2 SMA
Contoh soal 1
Sebuah peluru ditembakkan dengan kecepatan awal Vo = 50 m/s
dan sudut elevasi 45⁰.
a. berapa ketinggian maks yang dapat dicapai peluru?
b. hitung laju peluru ketika sampai di tanah
Di titik O, kecepatan peluru adalah Vo (ada angka angkanya)
Di titik puncak P, kecepatan peluru Vp = Vo. cos α (karena
Vy = 0)
a. H maks dapat dicari dengan hukum kekekalan energy, yaitu:
EM di O = EM di P
m.g.ho + ½ m. Vo² = m.g. hmax + ½ m. (Vo. cos α)²
0 + ½ m. Vo² = m.g.
hmax + ½ m. (Vo. cos α)²
coret m
− g. hmax = ½ (Vo. cos α)² - ½ .Vo²
− g. hmax = ½ Vo² (cos²α – 1) (ingat: sin²α + cos²α = 1)
g. hmax = ½ Vo² (1 − cos²α) (1 − cos²α = sin²α)
b. Mencari VB
EM di O = EM di B
m.g. ho + ½ . m. Vo² = m.g. hB + ½ .m. VB²
0 + ½ . m. Vo² = 0 + ½ . m. VB²
Vo = VB = 50 m/s
Contoh soal 2
Sebuah benda bermassa 1 kg meluncur ke bawah melalui
lintasan berbentuk busur seperempat lingkaran. Jari-jari lingkaran 2 meter.
a. Jika benda dilepaskan dari A dan lintasan licin, hitung
kecepatan benda saat di B
b. Jika bidang tersebut mempunyai gesekan, ternyata
kecepatan benda di B 4 m/s. Hitunglah usaha yang dilakukan oleh gesekan tsb!
Jawab:
a. Menghitung kecepatan di B
EM di A = EM di B
m.g. hA + ½ . m. VA² = m.g. hB + ½ .m. VB²
g. hA + 0 = 0 + ½ . VB² (VA = 0, meluncur bebas)
VB² = 2.g.hA
VB² = 2. 10. 2
VB² = 40
VB = 2√10
m/s
b. Menghitung usaha yang dilakukan karena adanya gaya gesek
EM di A = m.g. hA + ½ . m. VA² = 1. (10). 2 + ½ . 1. 0 = 20 joule
EM di B = m.g. hB + ½ .m. VB² = 0 + ½
. 1. 4² = 8 joule
Maka ada energy yang hilang sebesar 12 Joule.
Energi yang hilang ini diakibatkan adanya gaya gesekan yang
besar.
Contoh soal 3
Sebuah benda dengan massa 40 kg meluncur ke bawah sepanjang
bidang miring yang membentuk sudut 30⁰
terhadap bdang horizontal. Hitung usaha yang dilakukan gaya berat jika benda
bergeser 2 meter.
Cara 1
Benda meluncur ke bawah akibat adanya mg. sin 30⁰.
Maka gaya yang bekerja hanyalah F = mg. sin 30⁰.
Usaha = gaya x jarak
W = mg. sin 30⁰
x S
W = 40. (10). ½ x 2 = 400 Joule
Cara 2
Contoh 3
Suatu pegas (massa diabaikan) jika diberi gaya 100 N akan
menekan sejauh 1 meter. Pegas ini diletakkan di dasar bidang miring (gesekan
diabaikan). (α = 30⁰).
Suatu balok dengan massa 10 kg dilepas dari puncak bidang
miring. Pegas tertekan sejauh 2 meter.
a. Hitung jarak yang ditempuh balok dari posisi awal hingga posisi akhir
b. Hitung kecepatan benda pada saat mulai menyentuh pegas
Jawab:
Hitung konstanta pegas = k
Pegas à jika diberi F = 100 N maka akan tertekan sejauh x =
1 meter
F = k.x
100 = k. 1
k = 100 N/m
a. Mencari jarak L
Di titik A à Va = 0, hA = h
Di titik B à Vb = 0 (benda sesudah menekan akan berhenti
seketika) dan hB = 0
Saat terkena balok pegas tertekan = 2 meter. Maka usaha yang
mengenai pegas = ½ kx²
EM di A = EM di B
m.g. hA + ½ . m. VA² = m.g. hB
+ ½ kx² + ½ . m.VB²
10.(10). h + 0 = 0 + ½ . 100. (2²) + 0
100 h = 200
h = 2 meter
Dari h, jarak L bisa ditentukan
h/L = sin 30o
2/L = 1/2
L = 4 meter
Maka balok telah bergerak sejauh 4 meter
h/L = sin 30o
2/L = 1/2
L = 4 meter
Maka balok telah bergerak sejauh 4 meter
b. Mencari kecepatan balok saat menyentuh pegas (di C) saat pegas belum tertekan
Pegas tertekan sejauh 2 meter

Jawab;
h = 2 x ½ = 1 meter
EM di A = EM di C
m.g.hA + ½ .m. VA² = m.g.hC
+ ½ .m. VC²
10. (10). 1 + 0 = 0 + ½ .10. VB²
5. VC² = 100
VC² = 20
Vc = √20 = 2√5 m/s












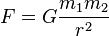


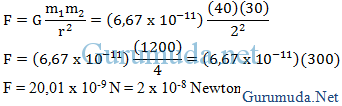 2. Berapa besar gaya gravitasi antara bumi dan bulan ?
2. Berapa besar gaya gravitasi antara bumi dan bulan ?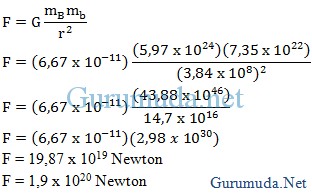 3. Pada jarak berapa dari bumi, besar gaya gravitasi antara bumi dan bulan bernilai nol ?
3. Pada jarak berapa dari bumi, besar gaya gravitasi antara bumi dan bulan bernilai nol ?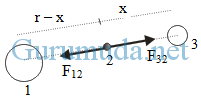 Keterangan :
Keterangan :
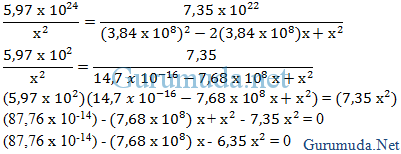








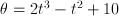 Tentukan:
Tentukan: